

There is no test statistic instead, you directly calculate the probability of obtaining the observed data under the null hypothesis. Sample size for testing differences in proportions for the paired-sample design. Exact tests, such as the exact test of goodness-of-fit, are different.
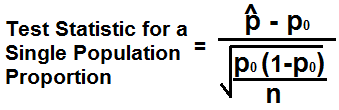
(Power = pnorm(x1)+pnorm(x2)) References Connor R.
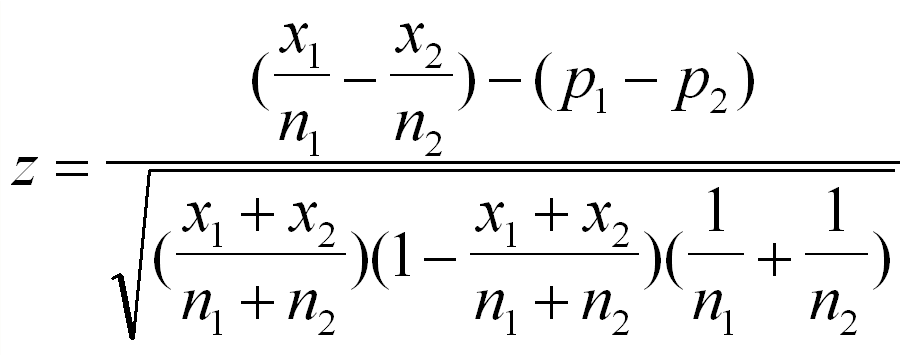
Suppose that our sample consists of pairs of subjects, and that each pair contains a subject from group 'A' and a subject from group 'B'.įurther suppose that we wish to compare the probability that an event occurs in group 'A' to that in group 'B'.Įxample study designs include matched case-control studies and cross-over studies.Ĭonceptually, the data can be listed as in the following table. Our null hypothesis is that the population proportions of all dichotomous variables 0.5. pwr source code: getAnywhere(pwr.2p.This calculator is useful for tests comparing paired proportions. This other SE question outlining the 2 methods of calculating powerģ. Test at significance level 0.10 the claim that there is no difference in proportion between boys and girls. You can also choose whether the calculator should determine the p-value from Z-test, or youd rather use the critical value.

Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. Documentation on pwr using the arcsin transformationĢ. This Z-test calculator is a tool that helps you perform a one-sample Z-test on the populations mean.
HYPOTHESIS TEST CALCULATOR PROPORTION FULL
But if you use the full number string, you would get the same numbers as pwr:ġ. n 0.05 N, where n is the sample size and N is the size of the population. The sample was obtained through a simple random sample process. Our main goal is in finding the probability of a difference between a sample mean p and the claimed value of the population proportion, p0. Note: numbers have been truncated for brevity. Hypothesis Test for a Population Proportion. Power = 1 - scs.norm(0, 1).cdf(3.482) + (scs.norm(0, 1).cdf(-0.437)) = 0.331059 On Macs, if you specify the count rather than the sample proportion, press the Return key before using the Calculate. Even in certain areas of electronics, it could be useful. Based on this, we can calculate the estimator of $p_i$ as: Hypothesis testing can be used for any type of science to show whether we reject or accept a hypothesis based on quantitative computing. Let's assume the true value of $p_1$ = 0.69 and that the true value of $p_2$ = 0.68. The null and alternative hypotheses are below and I'm using a significance level, $\alpha$ = 0.05 If you did not have such a prior hypothesis, and you only aim to test for a possible difference between the means, you need to do a double-sided test in this case you would mostly multiply the p-value by two. I'm trying to compute the power of a proportion test by hand. Use our proportions test template to compute a confidence interval and perform a hypothesis test of the proportion. This tutorial covers the steps for calculating hypothesis tests and confidence intervals for a single proportion in StatCrunch. In one-sided tests it is assumed that before doing the test you had a hypothesis that one mean of the two means was bigger than the other mean, i.e.


 0 kommentar(er)
0 kommentar(er)
